Market Segmentation - PCA & K-Means Clustering

Author

Collin Real

Published

July 26, 2024

Import Libraries

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy
from sklearn.preprocessing import StandardScaler
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.cluster import KMeans
pd.set_option('display.max_columns', None)

sns.set()

Import Data

df_customers = pd.read_csv('customers.csv')
df_customers

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
0	100000001	0	0	67	2	124670	1	2
1	100000002	1	1	22	1	150773	1	2
2	100000003	0	0	49	1	89210	0	0
3	100000004	0	0	45	1	171565	1	1
4	100000005	0	0	53	1	149031	1	1
...	...	...	...	...	...	...	...	...
1995	100001996	1	0	47	1	123525	0	0
1996	100001997	1	1	27	1	117744	1	0
1997	100001998	0	0	31	0	86400	0	0
1998	100001999	1	1	24	1	97968	0	0
1999	100002000	0	0	25	0	68416	0	0

2000 rows × 8 columns

Descriptive Statistics

df_customers.describe()

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
count	2.000000e+03	2000.000000	2000.000000	2000.000000	2000.00000	2000.000000	2000.000000	2000.000000
mean	1.000010e+08	0.457000	0.496500	35.909000	1.03800	120954.419000	0.810500	0.739000
std	5.774946e+02	0.498272	0.500113	11.719402	0.59978	38108.824679	0.638587	0.812533
min	1.000000e+08	0.000000	0.000000	18.000000	0.00000	35832.000000	0.000000	0.000000
25%	1.000005e+08	0.000000	0.000000	27.000000	1.00000	97663.250000	0.000000	0.000000
50%	1.000010e+08	0.000000	0.000000	33.000000	1.00000	115548.500000	1.000000	1.000000
75%	1.000015e+08	1.000000	1.000000	42.000000	1.00000	138072.250000	1.000000	1.000000
max	1.000020e+08	1.000000	1.000000	76.000000	3.00000	309364.000000	2.000000	2.000000

Variable correlation

df_customers.corr()

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
ID	1.000000	0.328262	0.074403	-0.085246	0.012543	-0.303217	-0.291958	-0.378445
Sex	0.328262	1.000000	0.566511	-0.182885	0.244838	-0.195146	-0.202491	-0.300803
Marital status	0.074403	0.566511	1.000000	-0.213178	0.374017	-0.073528	-0.029490	-0.097041
Age	-0.085246	-0.182885	-0.213178	1.000000	0.654605	0.340610	0.108388	0.119751
Education	0.012543	0.244838	0.374017	0.654605	1.000000	0.233459	0.064524	0.034732
Income	-0.303217	-0.195146	-0.073528	0.340610	0.233459	1.000000	0.680357	0.490881
Occupation	-0.291958	-0.202491	-0.029490	0.108388	0.064524	0.680357	1.000000	0.571795
Settlement size	-0.378445	-0.300803	-0.097041	0.119751	0.034732	0.490881	0.571795	1.000000

Correlation - Heat Map

plt.figure(figsize=(12, 9))
s = sns.heatmap(df_customers.corr(),
                annot=True,
                cmap='RdBu',
                vmin=-1,
                vmax=1)
s.set_xticklabels(s.get_xticklabels(), rotation=90)
plt.title('Correlation Matrix')
plt.show()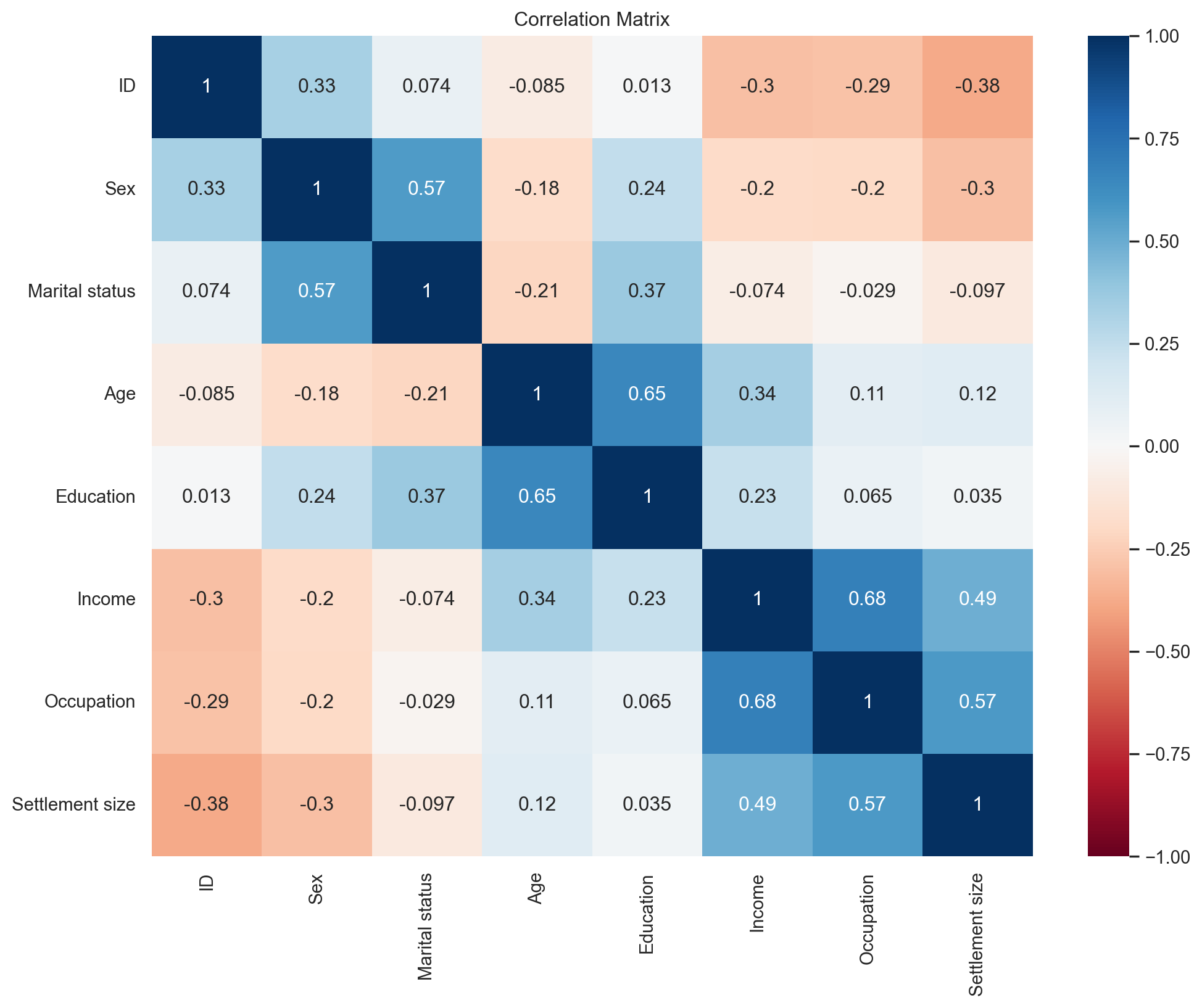

Scatter Plot - Age vs. Income

plt.figure(figsize=(12, 9))
# plt.scatter(df_customers.iloc[:, 2], df_customers.iloc[:, 4])
plt.scatter(df_customers['Age'], df_customers['Income'])
plt.xlabel('Age')
plt.ylabel('Income')

Text(0, 0.5, 'Income')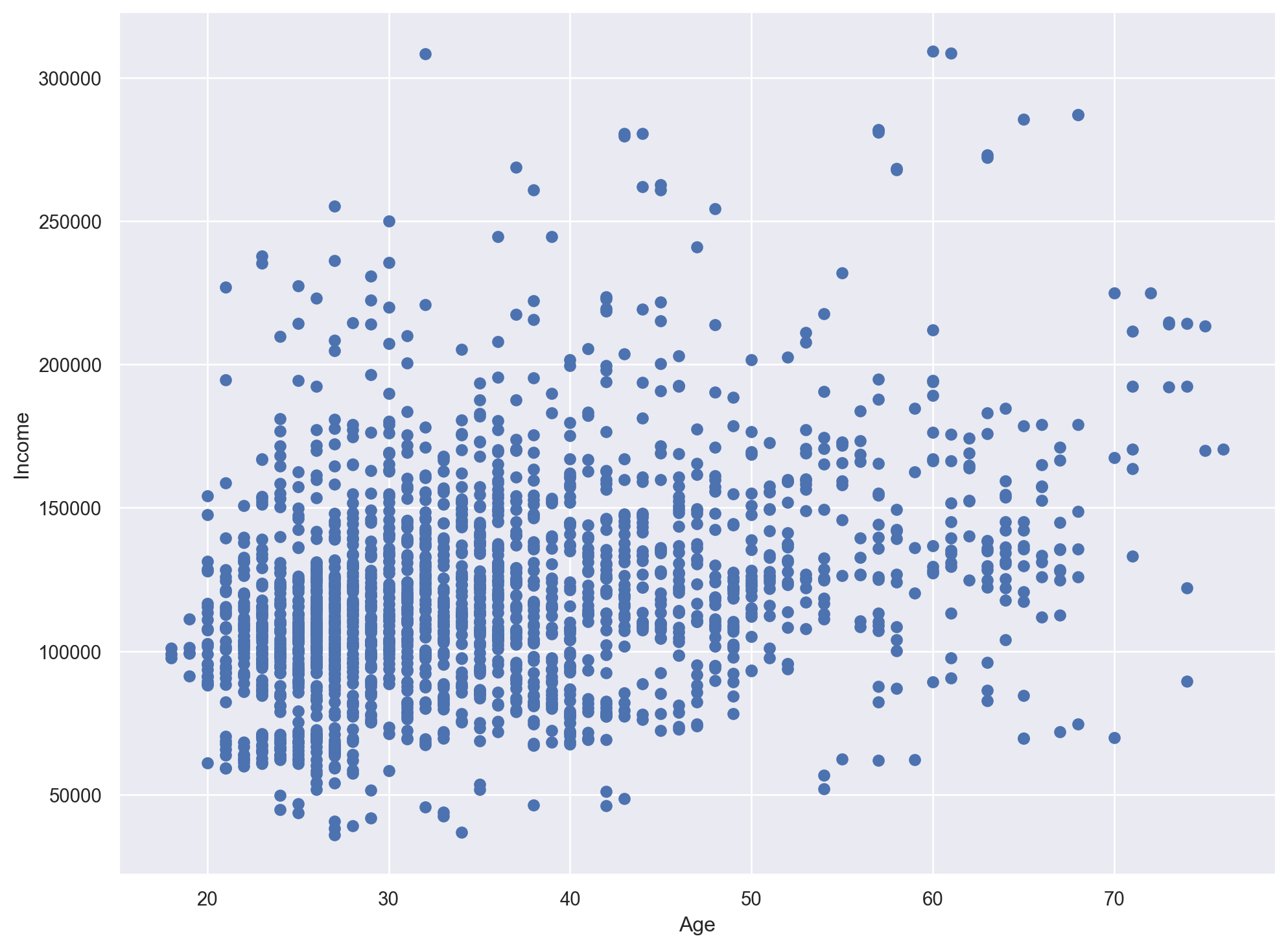

Standardize the DataFrame

scaler = StandardScaler()
customers_std = scaler.fit_transform(df_customers)
customers_std

array([[-1.731185  , -0.91739884, -0.99302433, ...,  0.09752361,
         0.29682303,  1.552326  ],
       [-1.72945295,  1.09003844,  1.00702467, ...,  0.78265438,
         0.29682303,  1.552326  ],
       [-1.7277209 , -0.91739884, -0.99302433, ..., -0.83320224,
        -1.26952539, -0.90972951],
       ...,
       [ 1.7277209 , -0.91739884, -0.99302433, ..., -0.90695688,
        -1.26952539, -0.90972951],
       [ 1.72945295,  1.09003844,  1.00702467, ..., -0.60332923,
        -1.26952539, -0.90972951],
       [ 1.731185  , -0.91739884, -0.99302433, ..., -1.3789866 ,
        -1.26952539, -0.90972951]])

Hierarchical Clustering

h_cluster = linkage(customers_std, method='ward')

plt.figure(figsize=(12, 9))
plt.xlabel('Observations')
plt.ylabel('Distance')
dendrogram(h_cluster,
           show_leaf_counts=False,
           no_labels=True)
plt.show()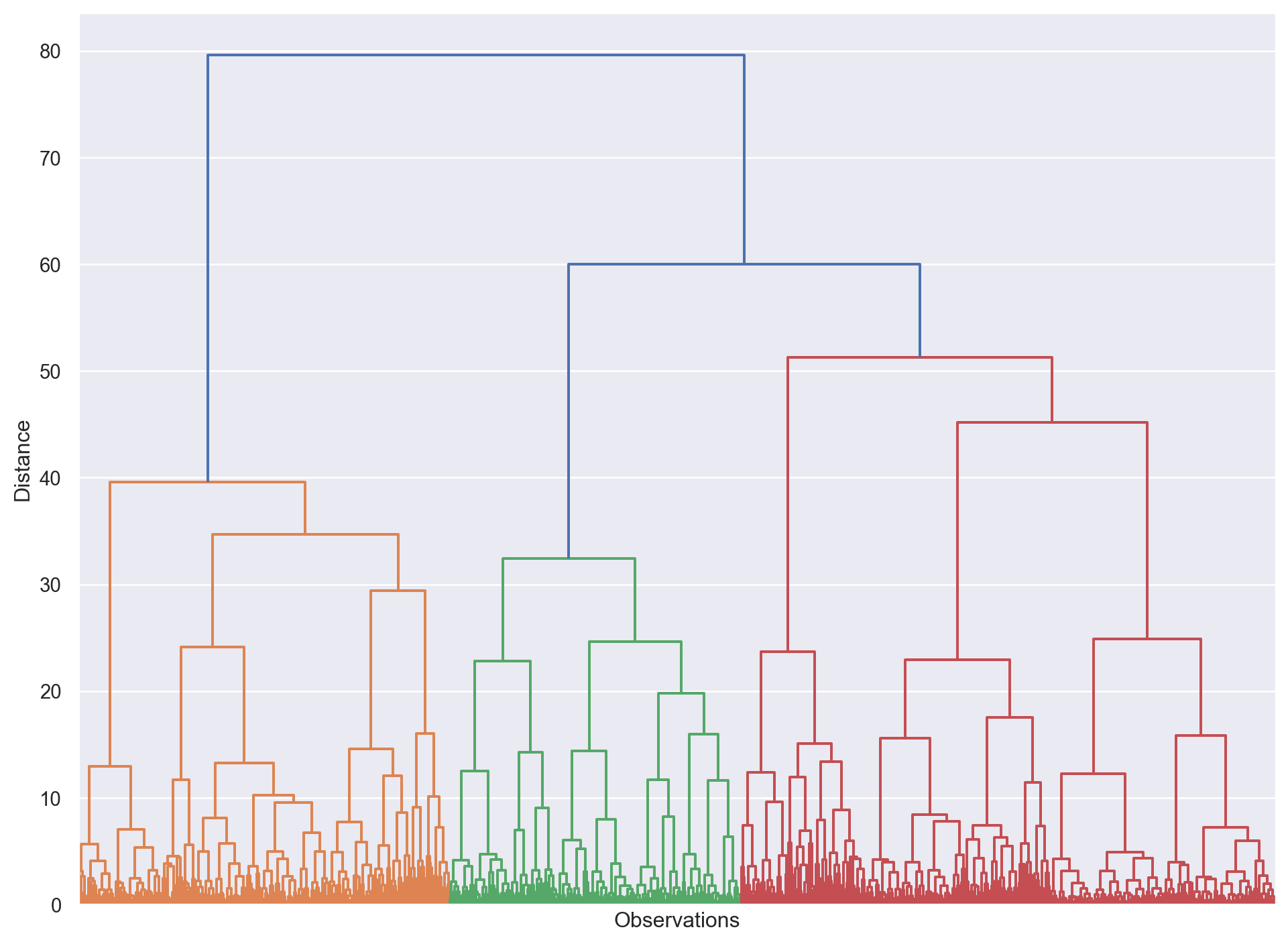

K-Means Clustering

results = {}

for i in range (1, 11):
    kmeans = KMeans(n_clusters=i, init='k-means++', random_state=42)
    kmeans.fit(customers_std)
    results[i] = kmeans.inertia_

plt.figure(figsize=(12, 9))
plt.plot(results.keys(), results.values(), marker='o', linestyle='--')
plt.plot([0.7, 3.2], [12000, 7000], color='#FF8400')
plt.plot([4.5, 9], [5700, 4000], color='#FF8400')
plt.xlabel('Number of Clusters')
plt.ylabel('Sum of squared distance')
plt.show()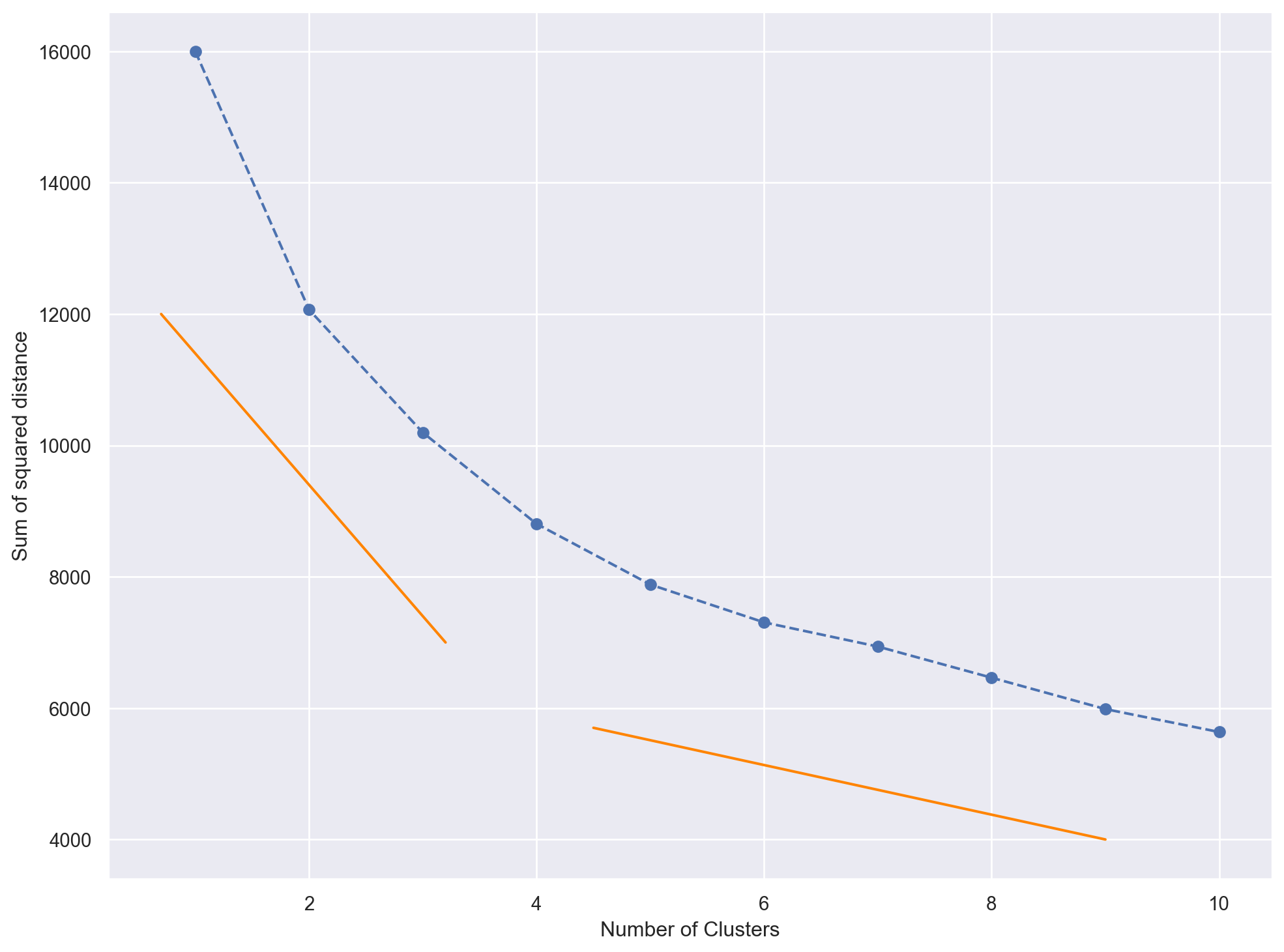

K-Means Clustering - 4 Clusters

kmeans = KMeans(n_clusters=4, init='k-means++', random_state=42)
kmeans.fit(customers_std)

df_customers_kmeans = df_customers.copy()
df_customers_kmeans['Segment'] = kmeans.labels_
df_customers_kmeans

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	Segment
0	100000001	0	0	67	2	124670	1	2	2
1	100000002	1	1	22	1	150773	1	2	1
2	100000003	0	0	49	1	89210	0	0	3
3	100000004	0	0	45	1	171565	1	1	0
4	100000005	0	0	53	1	149031	1	1	0
...	...	...	...	...	...	...	...	...	...
1995	100001996	1	0	47	1	123525	0	0	3
1996	100001997	1	1	27	1	117744	1	0	1
1997	100001998	0	0	31	0	86400	0	0	3
1998	100001999	1	1	24	1	97968	0	0	1
1999	100002000	0	0	25	0	68416	0	0	3

2000 rows × 9 columns

Characteristics of the people in each cluster

df_customers_analysis = df_customers_kmeans.groupby('Segment').mean().round(3)
df_customers_analysis

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
Segment
0	1.000007e+08	0.032	0.180	35.637	0.738	140135.807	1.251	1.389
1	1.000011e+08	0.876	0.999	29.003	1.068	105597.536	0.630	0.418
2	1.000009e+08	0.483	0.680	55.881	2.130	155931.141	1.093	1.078
3	1.000014e+08	0.403	0.043	34.690	0.742	94407.322	0.255	0.060

df_customers_analysis['Count'] = df_customers_kmeans[['Segment', 'Sex']].groupby('Segment').count()
df_customers_analysis['%'] = df_customers_analysis['Count'] / df_customers_analysis['Count'].sum()
df_customers_analysis.rename(index={
    0: 'well-off',
    1: 'fewer-opportunities',
    2: 'standard',
    3: 'career-focused'
}, inplace=True)

df_customers_analysis

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	Count	%
Segment
well-off	1.000007e+08	0.032	0.180	35.637	0.738	140135.807	1.251	1.389	633	0.3165
fewer-opportunities	1.000011e+08	0.876	0.999	29.003	1.068	105597.536	0.630	0.418	679	0.3395
standard	1.000009e+08	0.483	0.680	55.881	2.130	155931.141	1.093	1.078	269	0.1345
career-focused	1.000014e+08	0.403	0.043	34.690	0.742	94407.322	0.255	0.060	419	0.2095

plt.figure(figsize=(8, 6))
s = sns.barplot(data=df_customers_analysis, x=df_customers_analysis.index, y='Count', palette=['g','c','r','m'])
plt.xlabel('Segment')
plt.ylabel('Population')
plt.show()

/var/folders/s3/h2qfnwzs63b1k1xft79tdnfw0000gn/T/ipykernel_94496/843998559.py:2: FutureWarning:



Passing `palette` without assigning `hue` is deprecated and will be removed in v0.14.0. Assign the `x` variable to `hue` and set `legend=False` for the same effect.

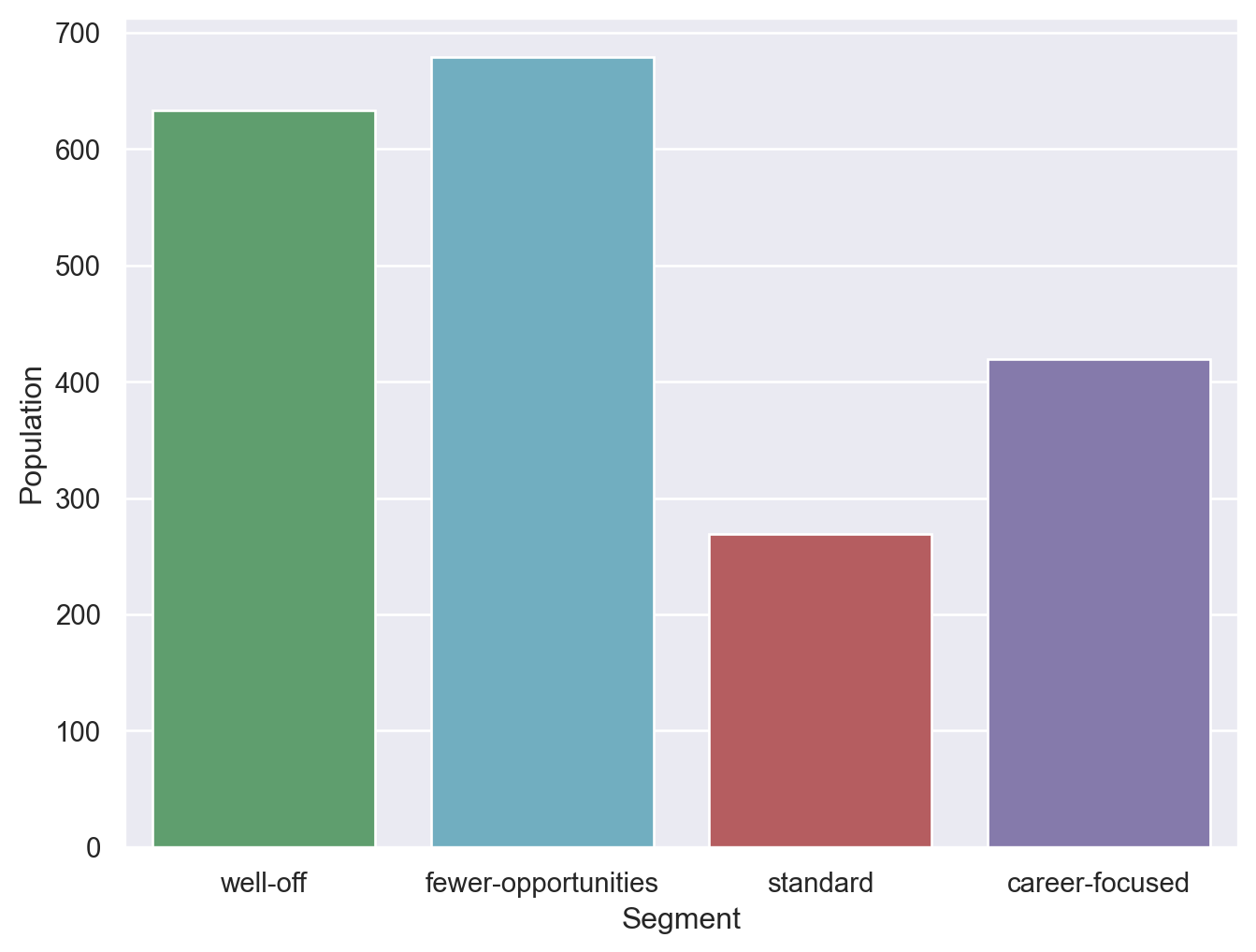
Assign Meaningful Labels to the segments

df_customers_kmeans['Segment'] = df_customers_kmeans['Segment'].map({
    0: 'well-off',
    1: 'fewer-opportunities',
    2: 'standard',
    3: 'career-focused'
})
df_customers_kmeans

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	Segment
0	100000001	0	0	67	2	124670	1	2	standard
1	100000002	1	1	22	1	150773	1	2	fewer-opportunities
2	100000003	0	0	49	1	89210	0	0	career-focused
3	100000004	0	0	45	1	171565	1	1	well-off
4	100000005	0	0	53	1	149031	1	1	well-off
...	...	...	...	...	...	...	...	...	...
1995	100001996	1	0	47	1	123525	0	0	career-focused
1996	100001997	1	1	27	1	117744	1	0	fewer-opportunities
1997	100001998	0	0	31	0	86400	0	0	career-focused
1998	100001999	1	1	24	1	97968	0	0	fewer-opportunities
1999	100002000	0	0	25	0	68416	0	0	career-focused

2000 rows × 9 columns

Visualize the segmented customers

colors = ['g','r','c','m']
sns.set_palette(sns.color_palette("pastel"))
plt.figure(figsize=(12, 8))
sns.scatterplot(
    x=df_customers_kmeans['Age'],
    y=df_customers_kmeans['Income'],
    hue=df_customers_kmeans['Segment'],
    palette=colors
)
plt.scatter(62, 160000 , s=60000, facecolors='none', edgecolors='#FF8400' ) 
plt.title('Age vs Income in each segment')

plt.show()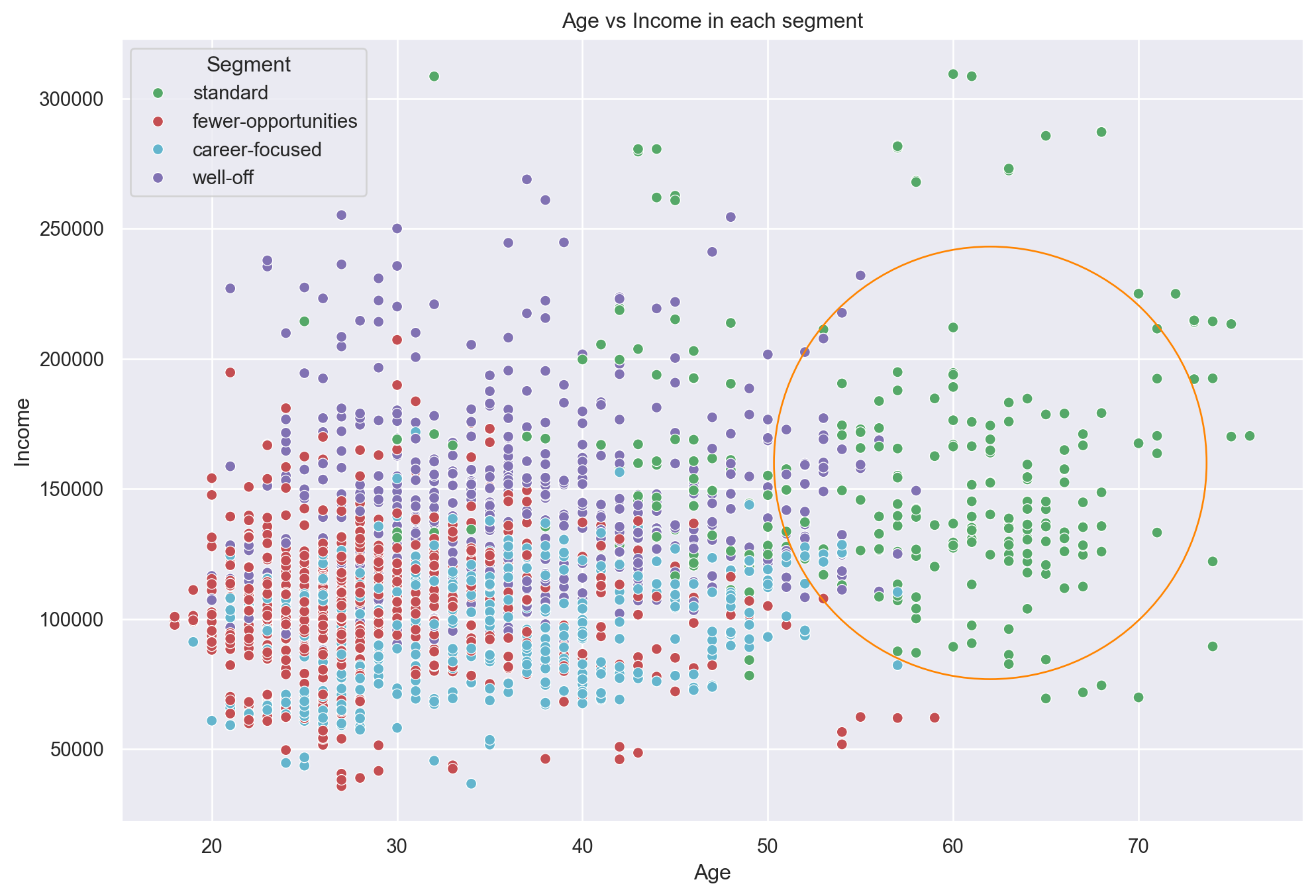

Education vs. Income

plt.figure(figsize=(16, 8))
sns.violinplot(
    x=df_customers_kmeans['Education'],
    y=df_customers_kmeans['Income'],
    hue=df_customers_kmeans['Segment'],
    palette=['g','r','c','m']
)
plt.title('Education vs Income in each segment')
plt.show()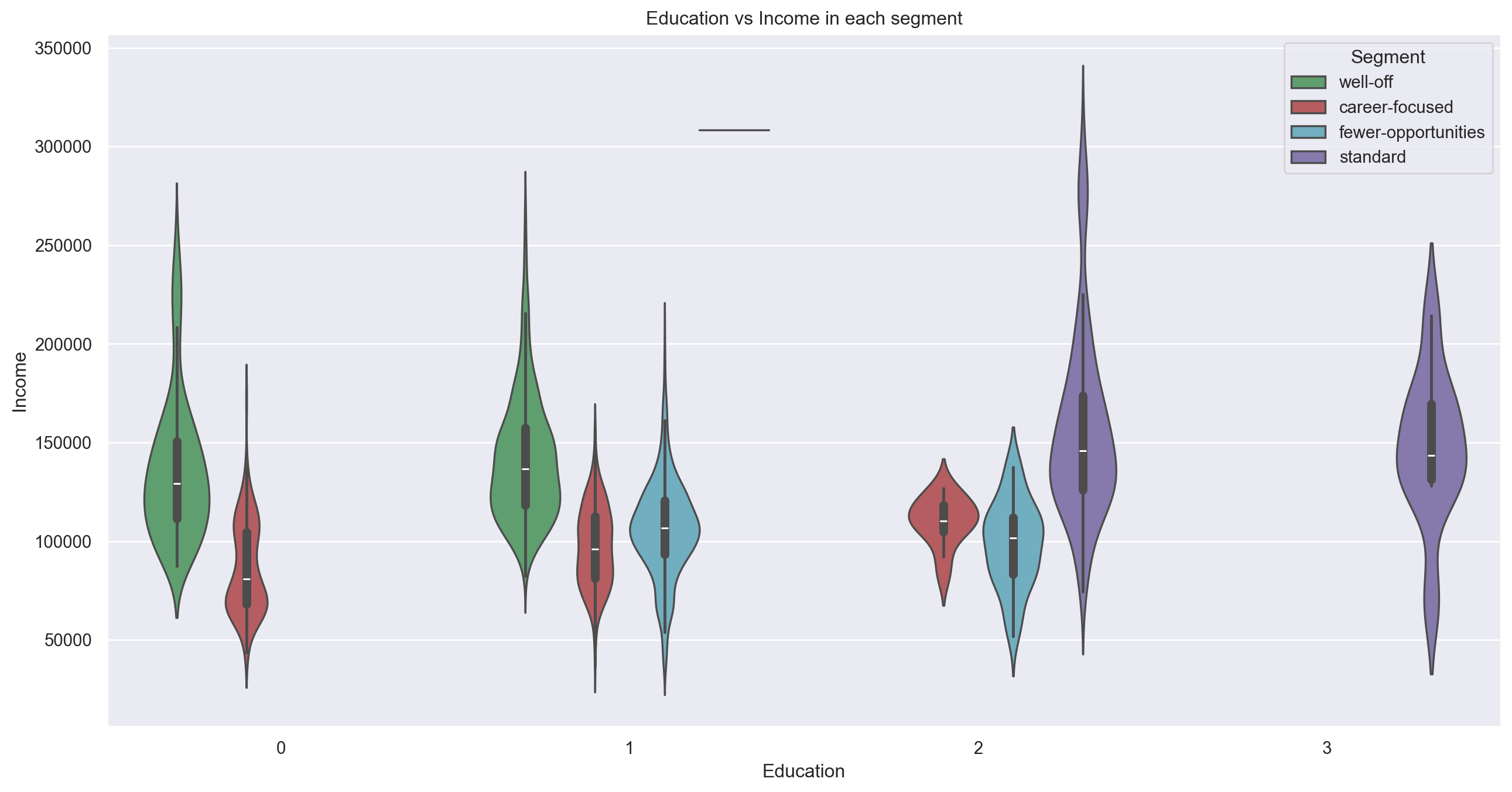

Improve K-Means with PCA

from sklearn.decomposition import PCA

pca = PCA()
pca.fit(customers_std)

pca.explained_variance_ratio_

array([0.34103573, 0.23178599, 0.16650585, 0.09955452, 0.06169548,
       0.04785186, 0.03407515, 0.01749541])

Plot the cumulative sum of variability

plt.figure(figsize=(12, 8))
plt.plot(range(0, 8), pca.explained_variance_ratio_.cumsum(), marker='o', linestyle='--')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')

Text(0, 0.5, 'Cumulative Explained Variance')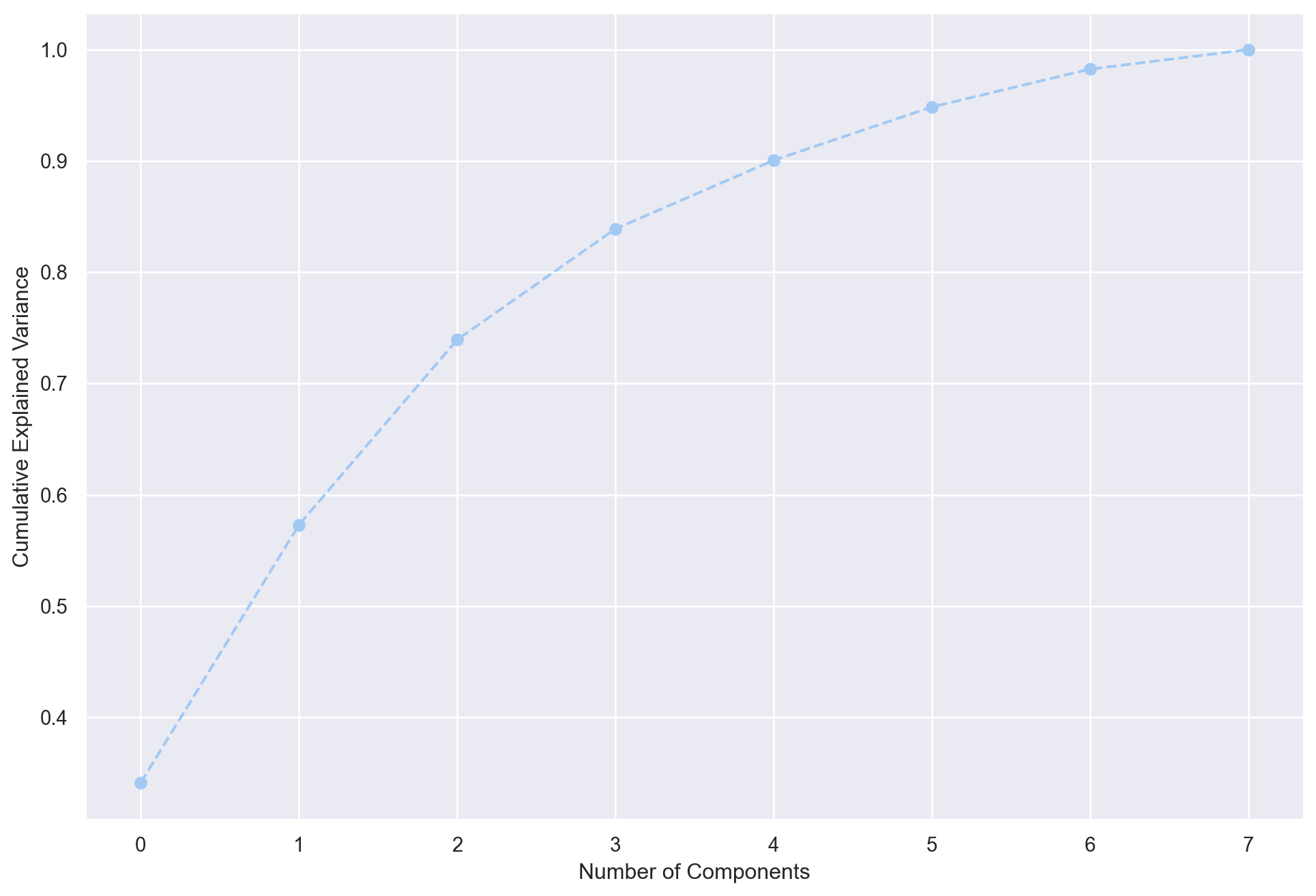

Pick 3 Components from the PCA model

pca = PCA(n_components=3)
pca.fit(customers_std)

df_pca_components = pd.DataFrame(
    data=pca.components_.round(4),
    columns=df_customers.columns.values,
    index=['component 1', 'component 2', 'component 3'])

df_pca_components

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
component 1	-0.3454	-0.3286	-0.1873	0.2703	0.1045	0.4838	0.4617	0.4543
component 2	0.1072	0.4213	0.4721	0.3553	0.6528	0.1763	0.0614	-0.0308
component 3	0.1435	-0.3180	-0.4854	0.6134	0.2523	-0.1236	-0.3446	-0.2621

Correlation Matrix of the 3 Components

s = sns.heatmap(
    df_pca_components,
    vmin=-1,
    vmax=1,
    cmap='RdBu',
    annot=True
)
plt.title('Correlation Matrix')
plt.show()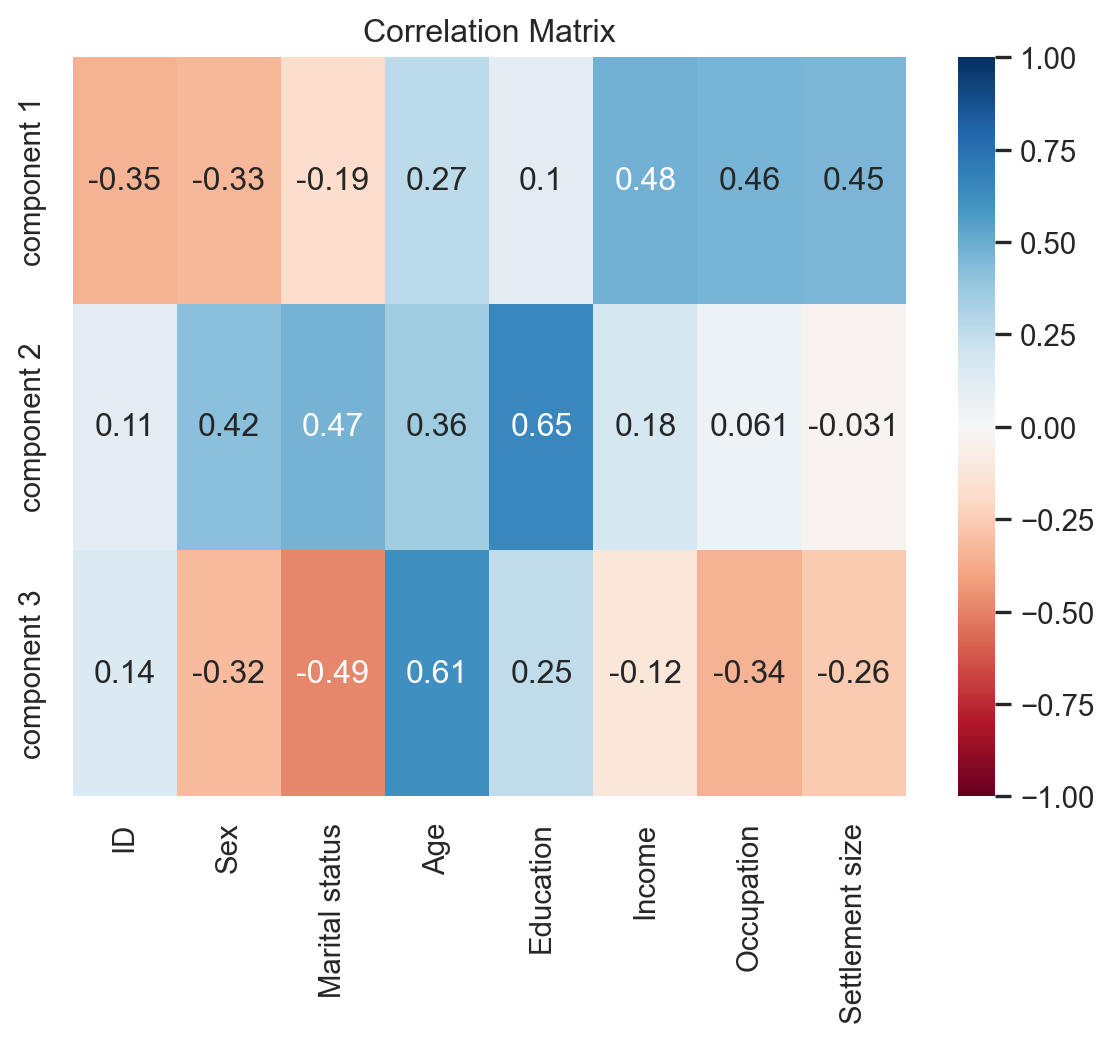

Implementing K-Means Clustering

pca_scores = pca.transform(customers_std)

results = {}

for i in range(1, 11):
    kmeans_pca = KMeans(n_clusters=i, init='k-means++', random_state=42)
    kmeans_pca.fit(pca_scores)   # pca_scores are standarzied by default
    results[i] = kmeans_pca.inertia_

plt.figure(figsize=(12, 8))
plt.plot(results.keys(), results.values(), marker='o', linestyle='--')
plt.xlabel('Number of Clusters')
plt.ylabel('Sum of squared distance')
plt.show()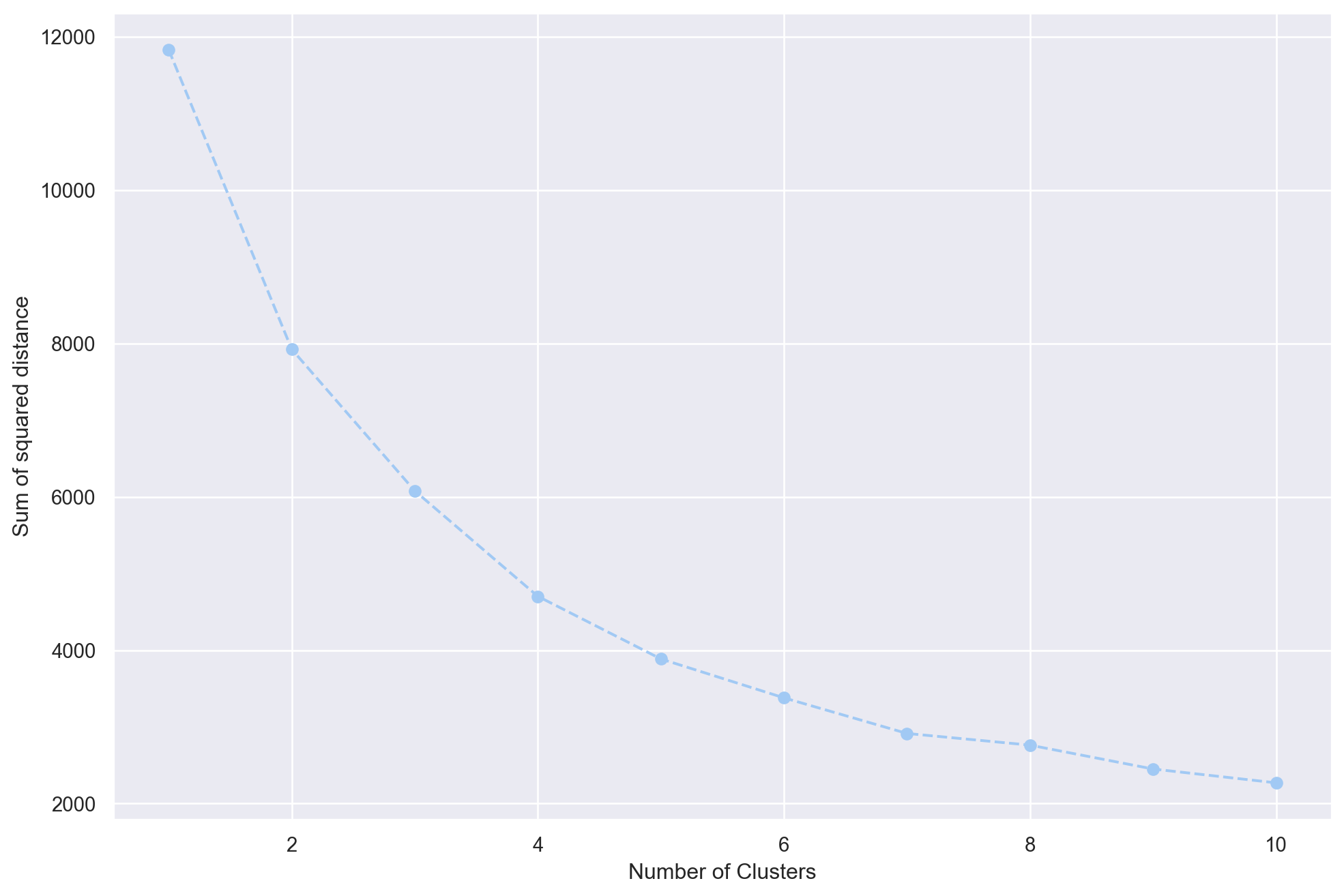

Implementing K-Means Clustering w/ 4 Clusters

kmeans_pca = KMeans(n_clusters=4, init='k-means++', random_state=42)
kmeans_pca.fit(pca_scores)

KMeans(n_clusters=4, random_state=42)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

df_segm_pca = pd.concat([df_customers.reset_index(drop=True), pd.DataFrame(pca_scores)], axis=1)
df_segm_pca.columns.values[-3:] = ['component 1', 'component 2', 'component 3']
df_segm_pca['K-means PCA'] = kmeans_pca.labels_
df_segm_pca.to_csv("customer_segment_pca.csv", encoding='utf-8', index=False)
df_segm_pca

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	component 1	component 2	component 3	K-means PCA
0	100000001	0	0	67	2	124670	1	2	2.859782	0.936676	2.036586	2
1	100000002	1	1	22	1	150773	1	2	0.944130	0.394492	-2.433785	0
2	100000003	0	0	49	1	89210	0	0	-0.023032	-0.881797	1.974083	3
3	100000004	0	0	45	1	171565	1	1	2.212422	-0.563616	0.635332	0
4	100000005	0	0	53	1	149031	1	1	2.110202	-0.425124	1.127543	0
...	...	...	...	...	...	...	...	...	...	...	...	...
1995	100001996	1	0	47	1	123525	0	0	-1.485348	0.432286	1.615196	3
1996	100001997	1	1	27	1	117744	1	0	-1.672129	0.839600	-0.923547	1
1997	100001998	0	0	31	0	86400	0	0	-1.841798	-2.158681	1.116012	3
1998	100001999	1	1	24	1	97968	0	0	-2.716832	0.561390	-0.476253	1
1999	100002000	0	0	25	0	68416	0	0	-2.209795	-2.423450	0.860709	3

2000 rows × 12 columns

Analyze Segmentation Results

df_segm_pca_analysis = df_segm_pca.groupby(['K-means PCA']).mean().round(4)
df_segm_pca_analysis

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	component 1	component 2	component 3
K-means PCA
0	1.000007e+08	0.0347	0.1924	35.4479	0.7382	140183.3155	1.2539	1.3912	1.4667	-0.9422	-0.1839
1	1.000012e+08	0.9190	0.9670	28.9580	1.0645	106617.4678	0.6597	0.4273	-1.2052	0.6160	-0.8333
2	1.000009e+08	0.4925	0.6842	55.8421	2.1278	157389.3872	1.1128	1.0977	1.5153	2.1581	0.8680
3	1.000013e+08	0.3418	0.1016	35.0462	0.7667	92501.5889	0.2079	0.0439	-1.2220	-0.8951	1.0196

Segment 0: low career and experience values with high education and lifestyle values.
Label: Standard
Segment 1: high career but low education, lifestyle and experience
Label: Career focused
Segment 2: low career, education and lifestyle, but high life experience
Label: Fewer opportunities
Segment 3: high career, education and lifestyle as well as high life experience
Label: Well-off

df_segm_pca_analysis['Count'] = df_segm_pca[['K-means PCA', 'Sex']].groupby(['K-means PCA']).count()
df_segm_pca_analysis['%'] = df_segm_pca_analysis['Count'] / df_segm_pca_analysis['Count'].sum()
df_segm_pca_analysis.rename(index={
    0: 'standard',
    1: 'career-focused',
    2: 'fewer-opportunities',
    3: 'well-off'
}, inplace=True)

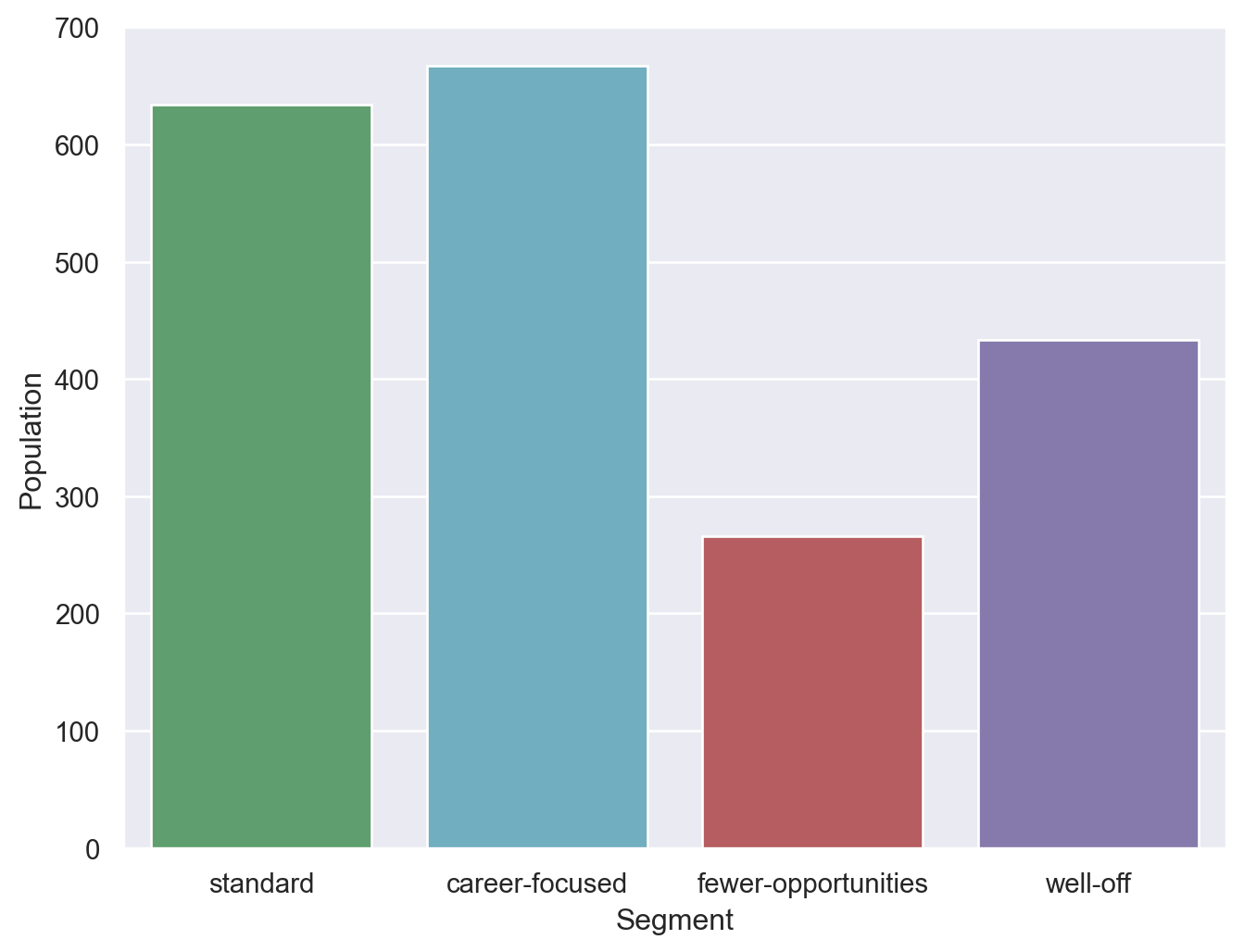
df_segm_pca_analysis

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	component 1	component 2	component 3	Count	%
K-means PCA
standard	1.000007e+08	0.0347	0.1924	35.4479	0.7382	140183.3155	1.2539	1.3912	1.4667	-0.9422	-0.1839	634	0.3170
career-focused	1.000012e+08	0.9190	0.9670	28.9580	1.0645	106617.4678	0.6597	0.4273	-1.2052	0.6160	-0.8333	667	0.3335
fewer-opportunities	1.000009e+08	0.4925	0.6842	55.8421	2.1278	157389.3872	1.1128	1.0977	1.5153	2.1581	0.8680	266	0.1330
well-off	1.000013e+08	0.3418	0.1016	35.0462	0.7667	92501.5889	0.2079	0.0439	-1.2220	-0.8951	1.0196	433	0.2165

Number of Customers per Segment

plt.figure(figsize=(8, 6))
s = sns.barplot(data=df_segm_pca_analysis, x=df_segm_pca_analysis.index, y='Count', palette=['g','c','r','m'])
plt.xlabel('Segment')
plt.ylabel('Population')
plt.show()

/var/folders/s3/h2qfnwzs63b1k1xft79tdnfw0000gn/T/ipykernel_94496/2239997931.py:2: FutureWarning:



Passing `palette` without assigning `hue` is deprecated and will be removed in v0.14.0. Assign the `x` variable to `hue` and set `legend=False` for the same effect.

Add segment labels to original dataset

df_segm_pca['Segment'] = df_segm_pca['K-means PCA'].map({
    0: 'standard',
    1: 'career-focused',
    2: 'fewer-opportunities',
    3: 'well-off'
})
df_segm_pca

	ID	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	component 1	component 2	component 3	K-means PCA	Segment
0	100000001	0	0	67	2	124670	1	2	2.859782	0.936676	2.036586	2	fewer-opportunities
1	100000002	1	1	22	1	150773	1	2	0.944130	0.394492	-2.433785	0	standard
2	100000003	0	0	49	1	89210	0	0	-0.023032	-0.881797	1.974083	3	well-off
3	100000004	0	0	45	1	171565	1	1	2.212422	-0.563616	0.635332	0	standard
4	100000005	0	0	53	1	149031	1	1	2.110202	-0.425124	1.127543	0	standard
...	...	...	...	...	...	...	...	...	...	...	...	...	...
1995	100001996	1	0	47	1	123525	0	0	-1.485348	0.432286	1.615196	3	well-off
1996	100001997	1	1	27	1	117744	1	0	-1.672129	0.839600	-0.923547	1	career-focused
1997	100001998	0	0	31	0	86400	0	0	-1.841798	-2.158681	1.116012	3	well-off
1998	100001999	1	1	24	1	97968	0	0	-2.716832	0.561390	-0.476253	1	career-focused
1999	100002000	0	0	25	0	68416	0	0	-2.209795	-2.423450	0.860709	3	well-off

2000 rows × 13 columns

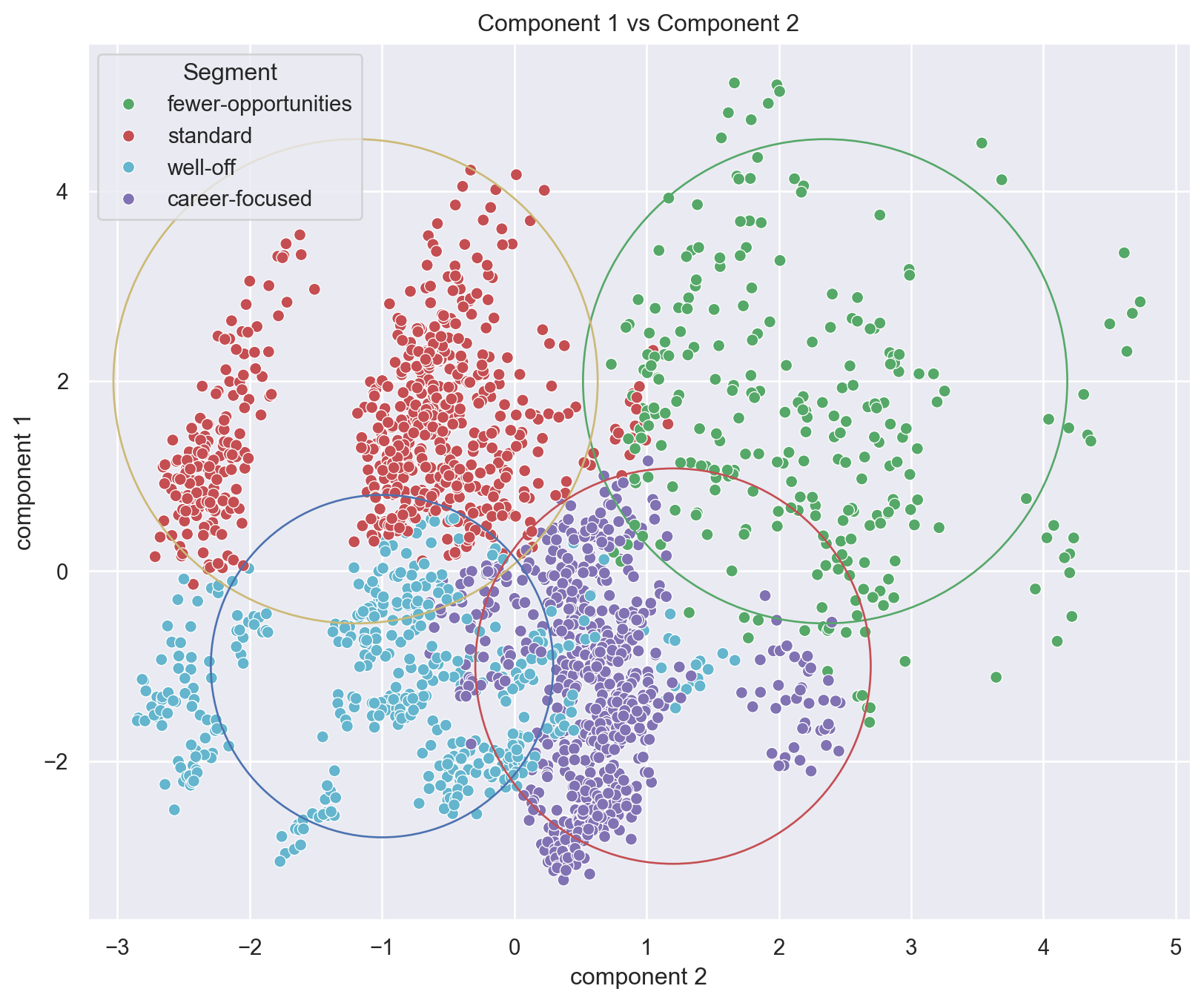
Visualize segments with respect to first two components

plt.figure(figsize=(10, 8))
sns.scatterplot(
    x=df_segm_pca['component 2'],
    y=df_segm_pca['component 1'],
    hue=df_segm_pca['Segment'],
    palette=['g','r','c','m']
)
plt.scatter(2.35, 2 , s=60000, facecolors='none', edgecolors='g' )
plt.scatter(-1.2, 2 , s=60000, facecolors='none', edgecolors='y' )
plt.scatter(-1, -1 , s=30000, facecolors='none', edgecolors='b' )
plt.scatter(1.2, -1 , s=40000, facecolors='none', edgecolors='r' )

plt.title('Component 1 vs Component 2')
plt.show()